[¯|¯] Il principio di indeterminazione di Heisenberg
Maggio 27th, 2017 | by Marcello Colozzo |
In un post precedente abbiamo esaminato il dualismo onda-corpuscolo, secondo cui la materia esibisce proprietà corpuscolari od ondulatorie in funzione della configurazione sperimentale atta a studiarne il comportamento.
Per "corpuscolo" intendiamo un qualunque sistema fisico avente dimensioni trascurabili rispetto a quelle dell'ambiente in cui si muove. Geometricamente, un corpuscolo è rappresentato da un punto dello spazio euclideo R³. Denominazioni alternative sono punto materiale e particella. Assegnato un sistema di riferimento inerziale K(Oxyz), supponiamo che siano note le equazioni orarie del moto, ossia consideriamo assegnata una rappresentazione parametrica regolare della traiettoria della particella, ove il parametro della rappresentazione è il tempo t misurato dall'orologio di K:
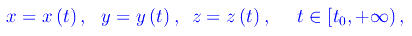
da cui è possibile ricavare - per derivazione rispetto a t - le componenti cartesiane del vettore velocità della particella in ogni istante di tempo:
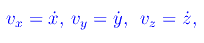
e quindi della quantità di moto (o impulso):
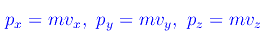
Orbene, il principio di interminazione di Heisenberg stabilisce:
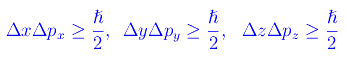
dove "h tagliato" è la costante ridotta di Planck, cioè pari alla costante di Planck divisa per 2π.
Senza formalizzarci troppo, diciamo che Δx,Δpx,..., esprimono l'incertezza con cui conosciamo la grandezza x (o px). Dalle disuguaglianze precedenti segue l'impossibilità di misurare simultaneamente e con precisione infinita, coppie di grandezze (x,px),(y,py),(z,pz). Ad esempio, se misuriamo la componente px dell'impulso con precisione infinita (Δpx=0), si ha Δx=+oo. Fisicamente questo risultato implica che la particella può avere un'ascissa qualunque (da -oo a +oo). Al contrario, possiamo misurare y,z con precisione infinita anche se Δpx=0, con la differenza che si avrà Δpy=Δpz=+oo, ovvero una indeterminazione sulle componenti py,pz del vettore impulso. Queste considerazioni (che nascono da evidenze sperimentali) distruggono il concetto di traiettoria. Fondamentalmente, le predette evidenze sperimentali nascono da due esperienze ideali proposte da Heisenberg, una delle quali è la seguente.
Tags: diffrazione, fenditura, principio di indeterminazione di Heisenberg
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico












By Giovanni D'Arienzo on Nov 8, 2017
veramente un brutto posto dove mettere la barra per condividere. non si riesce a leggere l'articolo.
By Marcello Colozzo on Nov 8, 2017
ho rimosso il plugin, almeno per ora. tanto non serve o altrimenti vedo di posizionarlo altrove. Grazie per la segnalazione