» Esercizi svolti di Matematica e Fisica

[¯|¯][Numeri primi] L'analisi di Riesel e Gohl (parte quarta)

Aprile 22nd, 2017 | by Marcello Colozzo |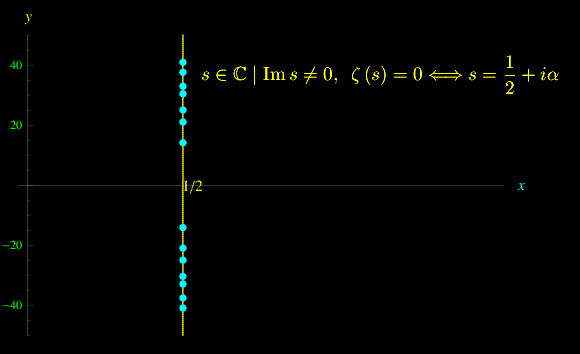

Per esplicitare la sommatoria

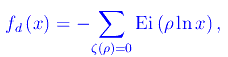
applichiamo la congettura di Riemann:

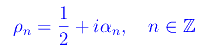
Si noti che l'espressione analitica della successione di elmenti di R:

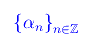
è ignota. Ciò che è invece noto, è l'insieme dei valori assunti dai singoli termini fino a un certo ordine. In parole povere la non conoscenza dell'espressione analitica (se esiste) della predetta successione, implica che la parte immaginaria degli zeri della funzione zeta di Riemann, può essere al più computata manualmente (o via software), e ciò può realizzarsi per un numero infinito di elementi. In ogni caso, consideriamo l'espansione da -oo a +oo:

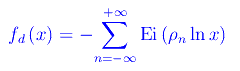
Per una nota proprietà della funzione zeta di Riemann:

dove ρ_n^* è il complesso coniugato di ρ_n:

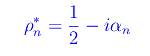
Cioè gli zeri della zeta di Riemann si distribuiscono lungo la linea critica per coppie complesse coniugate, da cui la simmetria della distribuzione rispetto all'asse reale, come appare in fig. 1. Ciò suggerisce la posizione:

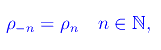
da cui

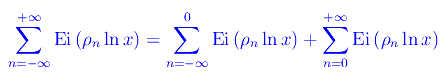
Se nella prima sommatoria eseguiamo il cambio di indice n'=-n:

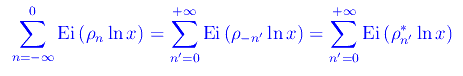
Cioè

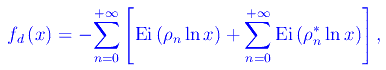
il cui contributo alla funzione di distribuzione dei primi π₀(x) è:

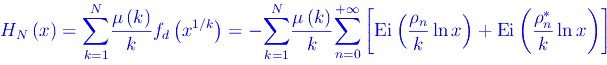
Ovvero

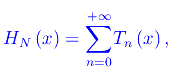
essendo

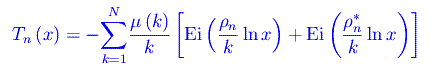
In altri termini, la funzione H_N(x) è per un assegnato N, il contributo alla funzione di distribuzione π₀(x), ed è la somma della serie scritta sopra, il cui termine n-esimo è il contributo proveniente dallo zero n-esimo della zeta di Riemann.

Sostienici

Tags: congettura di riemann, numeri primi, zeri non banali zeta di riemann

Articoli correlati