[¯|¯] Oscillazioni smorzate con legge esponenziale. Decremento logaritmico
Marzo 21st, 2017 | by Marcello Colozzo |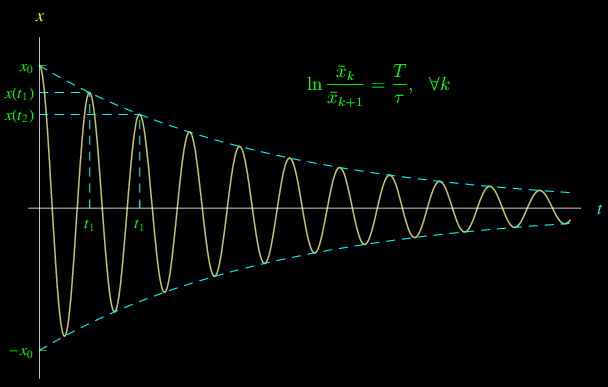
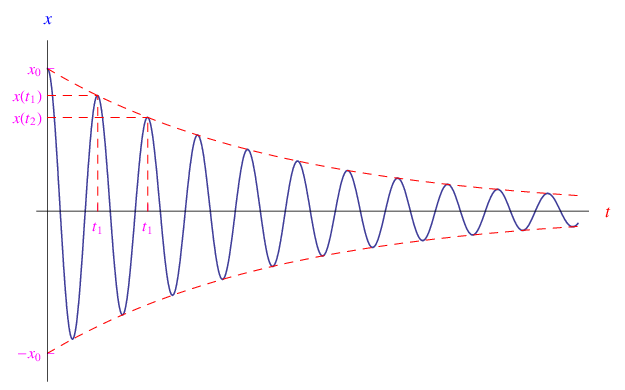
Fig. 1.Oscillazioni smorzate. L'ampiezza decresce con legge esponenziale, conservando il decremento logaritmico.
Caso oscillatorio smorzato (b < bcrit)
Prima di affrontare il caso n. 3 (oscillazioni smorzate), sintetizziamo i risultati raggiunti , in modo da comprendere la fisica che c'è dietro questo problema matematico. Innanzitutto riscriviamo l'equazione differenziale del moto nella forma:
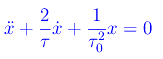
Ricordiamo che τ=(2m)/b è la costante di tempo della resistenza passiva, quindi delle forze di attrito. Abbiamo poi introdotto una nuova grandezza avente le dimensioni di un tempo:
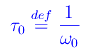
legata al periodo T0 delle oscillazioni armoniche in assenza di attrito, dalla relazione:
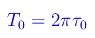
In altri termini, la grandezza τ0 fissa la scala dei tempi delle oscillazioni caratteristiche del sistema. Ne consegue che le condizioni di aperiodicità e di criticità si riscrivono:
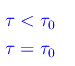
τ<τ0 significa che le forze di attrito sono più "efficienti" della forza elastica, giacché hanno una scala dei tempi minore. Per τ=τ0 si ha, invece, un equilibrio che da luogo al caso "critico" in cui il moto non è ancora oscillante.
È facile allora immaginare che la condizione
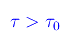
determina un moto oscillatorio, comunque smorzato dalle forze di attrito. Abbiamo poi la condizione estrema:
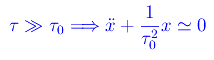
Cioè per grandi valori di τ (rispetto a τ0), quindi per piccoli valori del coefficiente di viscosità b, le soluzioni dell'equazione differenziale del moto si comportano come quelle dell'equazione
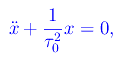
per cui si ha un'oscillazione armonica di pulsazione ω0=τ0-1. Nel limite opposto:
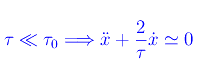
Cioè per piccoli valori di τ (rispetto a τ0), il moto è completamente dominato dalle forze di attrito.
Ciò premesso, consideriamo il caso
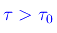
Con tale condizione l'equazione caratteristica ammette due radici complesse coniugate:
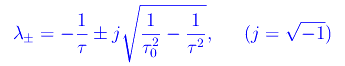
Osservazione. In questo lavoro utilizziamo il simbolo j per denotare l"unità immaginaria. Rammentiamo che tale convenzione è d'uso in Elettrotecnica ed in Elettronica per non creare confusione con il simbolo i che denota l'intensità di corrente.
Riscriviamo
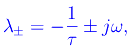
essendo:
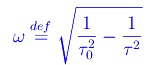
una grandezza con le dimensioni di una pulsazione. Risulta:
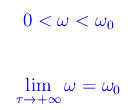
Cioè in assenza di attrito, ω è la pulsazione caratteristica. Un sistema fondamentale di integrali dell'equazione differenziale assegnata è
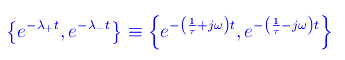
Pertanto l'integrale generale si scrive
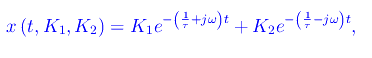
dove K1,K2 sono costanti arbitrarie. Sviluppando gli esponenziali complessi utilizzando la nota formula di Eulero, si ottiene:
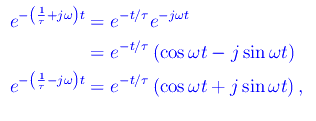
cosicché:
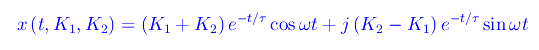
Cioè
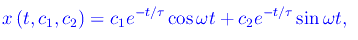
avendo definito le nuove costanti di integrazione:
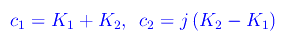
Derivando la x(t):
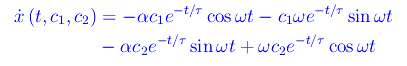
Le condizioni iniziali
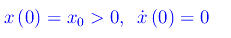
implicano
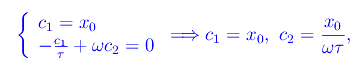
che sostituite nell'integrale generale:
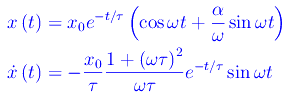
Per studiare l'andamento della funzione x(t) è conveniente scrivere la sua espressione nel seguente modo:
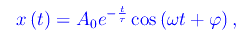
dove A0>0 ha le dimensioni di una lunghezza, mentre φ è la fase iniziale. Deve essere:
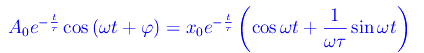
Sviluppando il coseno che compare a primo membro con le formule di addizione degli archi, si ha:
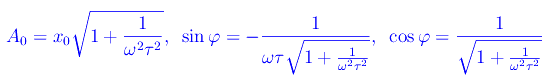
Riesce:
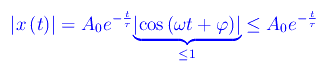
Cioè
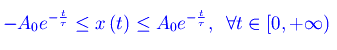
Dal momento che
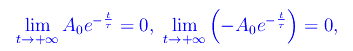
si ha per il teorema dei carabinieri:
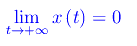
segue poi che il grafico di x(t) è inviluppato dalle curve esponenziali ±A0e-t/τ. La funzione x(t) presenta un numero infinito numerabile di massimi relativi nei punti tk tali che
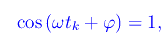
da cui
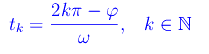
Quindi
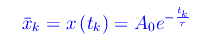
Per un assegnato k, il massimo relativo successivo è
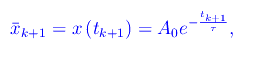
essendo
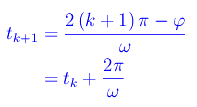
Abbiamo
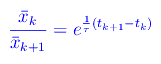
ovvero
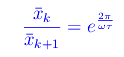
Passando ai logaritmi:
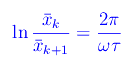
Poniamo
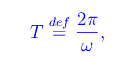
che non è il periodo di x(t) in quanto non periodica, bensì il tempo necessario affinchè l'ascissa dell'oscillatore passi dal valore x(tk) al valore x(tk+1)
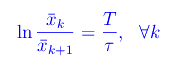
ed è pertanto una costante caratteristica dell'oscillatore, che si chiama decremento logaritmico. In figura riportiamo un tipico andamento:
Tags: attrito, decremento logaritmico, oscillatore armonico smorzato, resistenza passiva
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











