[¯|¯] Oscillazioni smorzate. Il caso aperiodico
Marzo 20th, 2017 | by Marcello Colozzo |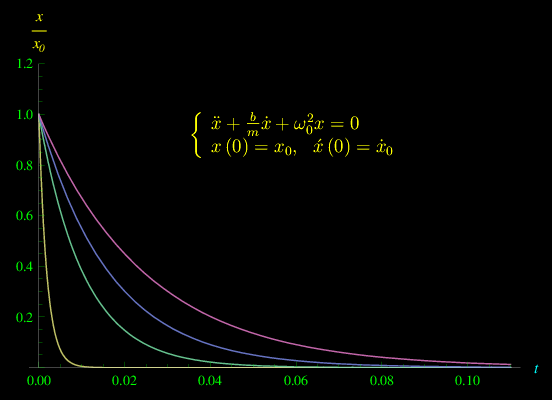
Fig. 1. Alcuni elementi della famiglia di soluzioni del problema di Cauchy relativo a un oscillatore armonico smorzato nel caso aperiodico.
Abbiamo studiato le oscillazioni libere e forzate di un punto materiale soggetto a una forza elastica unidimensionale nel caso ideale di assenza di resistenze passive. Un modello più realistico deve inglobare resistenze passive in grado di riprodurre la viscosità del mezzo in cui l'oscillatore si muove, nonché gli attriti interni nel materiale elastico che determina la forza di richiamo. Il caso matematicamente più semplice è il regime lineare in cui la predetta resistenza passiva è una funzione lineare ed omogenea della velocità scalare, ed è orientata in verso opposto al vettore velocità. Orientando un asse x nella direzione del moto con origine nella posizione di riposo e verso positivo coincidente con quello di allungamento della molla, il secondo principio della dinamica si scrive:
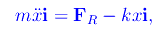
dove FR è la resistenza passiva.
Per quanto precede:
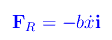
Qui b>0 è una costante nota come coefficiente di viscosità. Da ciò segue l'equazione differenziale del moto:
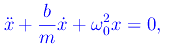
avendo già definito nei post precedenti la pulsazione caratteristica ω0=sqrt(k/m). La predetta equazione è un'equazione differenziale ordinaria (in forma normale) del secondo ordine, lineare ed omogenea. Condizioni iniziali assegnate, danno luogo al seguente problema di Cauchy:
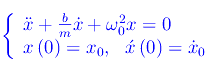
Determiniamo innanzitutto l'integrale generale. L'equazione caratteristica è
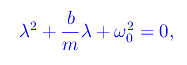
le cui radici sono
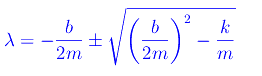
Distinguiamo i seguenti casi:

Caso aperiodico (b>bcrit)
Abbiamo due radici reali e distinte:
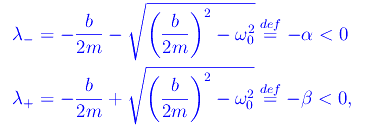
Cioè
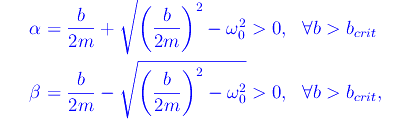
aventi le dimensioni dell'inverso di un tempo. Un sistema fondamentale di integrali dell'equazione differenziale assegnata è {ξ1(t),ξ2(t)}, dove
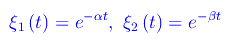
Ciò implica che l'integrale generale si scrive:
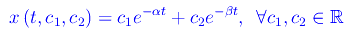
Introduciamo una grandezza caratteristica - cioè dipendente solo da b e m e non da una eventuale forza esterna:
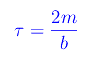
Tenendo conto della
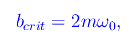
si ha
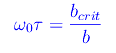
Quindi

che si chiama condizione di aperiodicità. Inoltre:
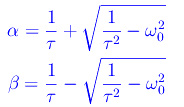
Derivando la funzione x(t) rispetto al tempo otteniamo il modulo della velocità:
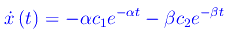
Imponendo le condizioni iniziali si perviene al sistema lineare omogeneo nelle incognite c1,c2:
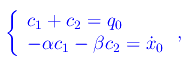
da cui
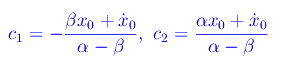
Prima di sostituire le costanti trovate nell'espressione dell'integrale generale, definiamo altre due grandezze con le dimensioni di un tempo:
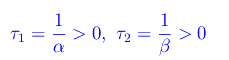
Cioè
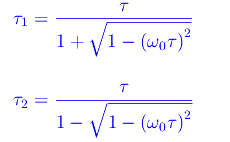
La realtà di tali grandezze è garantita dalla condizione di aperiodicità.
Finalmente otteniamo l'ascissa dell'oscillatore in funzione del tempo:
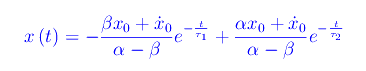
Alla stessa maniera otteniamo il modulo della velocità:
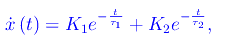
essendo
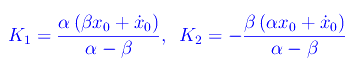
Per tracciare il grafico di x(t) l'algoritmo è il seguente: supponiamo di conoscere il valore di ω0. Dalla condizione di criticità:
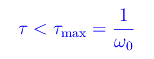
Ad esempio, per ω0=20rad/s, si ha
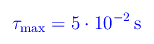
I valori di τ e ω00 determinano univocamente i valori di α e ß e quindi l'ascissa in funzione del tempo. In particolare, se la velocità iniziale è nulla, si ha:
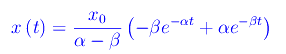
Il grafico di fig. 1 riporta l'andamento della funzione x(t) per differenti valori della costante di tempo τ.
Conclusione
Nel caso aperiodico, l'ascissa x(t) si annulla esponenzialmente, quindi senza compiere oscillazioni. Fisicamente, la x(t) può considerarsi nulla per istanti maggiori della costante di tempo τ per svariati ordini di grandezza.
Le considerazioni svolte si applicano nel caso circuitale, con le solite sostituzioni: alla massa inerziale m corrisponde il coefficiente di autoinduzione L, alla costante elastica della molla il reciproco della capacità del condensatore, e al coefficiente di viscosità b, la resistenza ohmica R. In tal caso, l'ascissa x è la carica elettrica.
Tags: attrito, caso aperiodico, oscillatore armonico smorzato, resistenza passiva
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











