» Esercizi svolti di Matematica e Fisica

[¯|¯] Forze variabili nel tempo (oscillatore armonico). Forme d'onda (circuito elettrico)

Marzo 19th, 2017 | by Marcello Colozzo |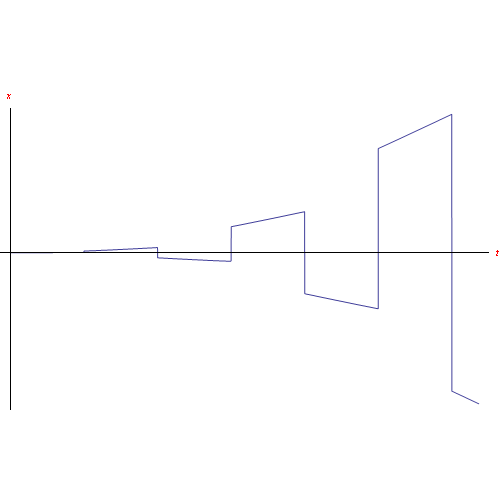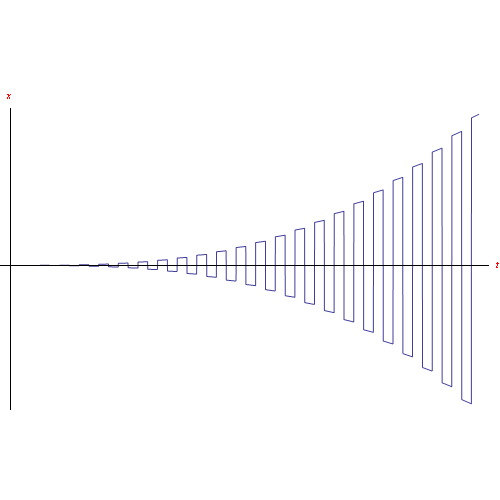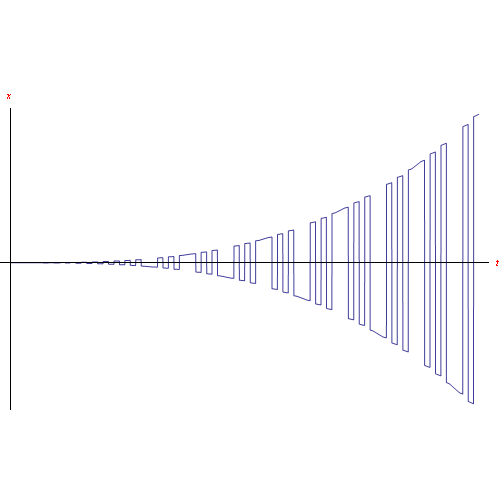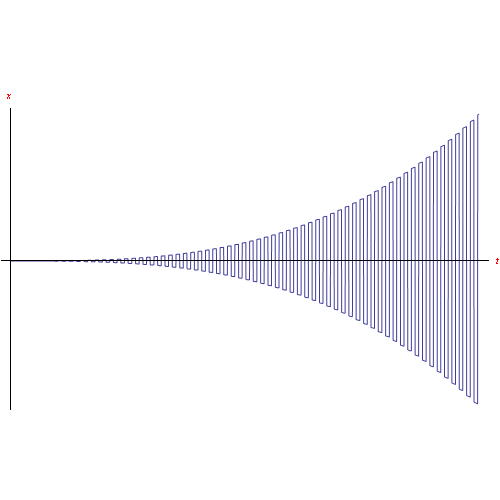

---

Studio della funzione f(x)=arccos(cosx)

Abbiamo esaminato il caso di un punto materiale di massa m sottoposto a una forza elastico di richiamo (caso unidimensionale) e ad una forza periodica del tempo:

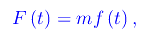
dove

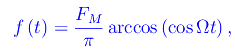
essendo Ω>0 la frequenza angolare (o pulsazione) di F(t). L'equazione differenziale del moto si scrive:

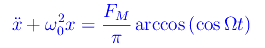
Ricordiamo che ω₀=(k/m)^1/2 è la pulsazione caratteristica dell'oscillatore. Notiamo poi che l'equivalente elettrico di tale sistema meccanico è un circuito i cui componenti sono rispettivamente un'induttanza di coefficiente di auto-induzione L e un condensatore di capacità C. Dal momento che ci troviamo in condizioni di idealità i.e. stiamo trascurando le forze di attrito nell'oscillatore meccanico, segue che nell'analogo elettrico il condensatore e l'induttanza non presentano una resistenza ohmica. Eseguendo la nota sostituzione:

si perviene all'equazione differenziale che regola l'andamento della carica elettrica:

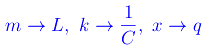
si perviene all'equazione differenziale che regola l'andamento della carica elettrica:

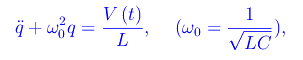
in cui abbiamo lasciata inespressa l'espressione analitica della funzione V(t) che è la f.e.m. che alimenta la serie LC (è il "corrispondente" della forza F(t) applicata all'oscillatore meccanico). Integrando la predetta equazione differenziale per assegnate condizioni iniziali, si perviene alla funzione q(t) e quindi all'intensità di corrente:









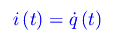
Qualche perplessità può insorgere dall'utilizzo della funzione:

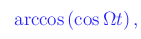
nel senso che si è portati erroneamente a scrivere (per definizione di funzione inversa

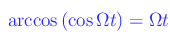
Per maggiore chiarezza riferiamoci al caso più astratto:

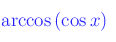
Osserviamo innanzitutto che le funzioni circolari sono invertibili solo localmente, ovvero in un qualunque intervallo di periodicità, in quanto non sono strettamente monotone su tutto l'insieme di definizione. Nel caso delle funzioni sin x e cos x ci si riferisce all'intervallo [-π, π].

Ciò premesso, studiamo la funzione:

• Insieme di definizione
  È manifestamente X=R, giacchè |cosΩx|<=1.
• Periodicità
  La funzione è periodica di periodo T=2π/&Omega, onde studiamo la funzione in
  
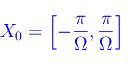
• Parità
  La funzione è pari, per cui Γ_f:y=f(x) è simmetrico rispetto all'asse y. Quindi studiamo la funzione in X'₀=[0,π/&Omega].
• Grafico
  Risulta
  
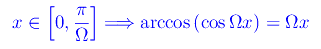
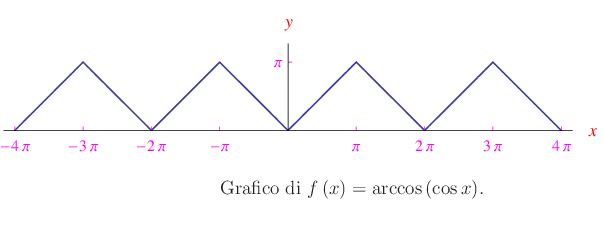
  Ne consegue che in X'₀ il grafico è il segmento di estremi (0,0) e A(π/&Omega,π). La simmetria rispetto all'asse y e la periodicità ci permettono di tracciare il grafico in R come riportato in figura.

Punto materiale sottoposto a una forza periodica del tempo

Ritorniamo al caso dell'oscillatore

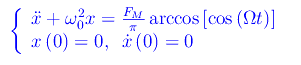
o al caso matematicamente equivalente della serie LC alimentata dalla f.e.m.

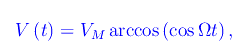
onde

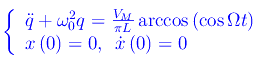
Avevamo visto che la soluzione segue l"andamento triangolare" solo per ω0->+oo. Consideriamo allora il caso particolare ω0=0 che descrive un punto materiale soggetto alla sola forza periodica F(t). Nel caso elettrico, ci corrisponde a C=0. Cioè abbiamo una induttanza alimentata dalla V(t). Per l'oscillatore meccanico l'equazione differenziale del moto può scriversi:

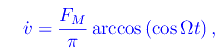
dove v è la velocità. Integrando otteniamo la posizione in funzione del tempo

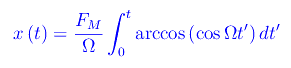
Calcoliamo l'integrale

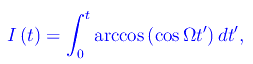
Eseguiamo dapprima il cambio di variabile

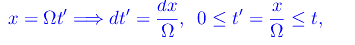
onde integriamo per parti:

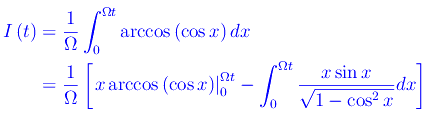
Osserviamo che

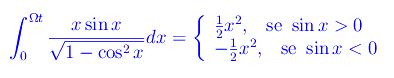
Cioè

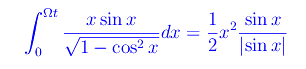
Segue

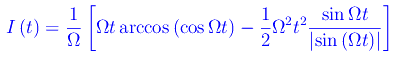
Quindi

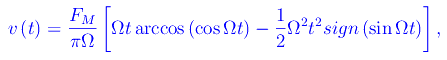
essendo sign è la funzione signum. In figura riportiamo l'andamento della velocità in funzione del tempo:

Per ricavare l'ascissa x(t):

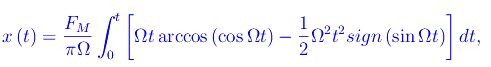
calcolo alquanto problematico. È allora preferibile affidarsi a Mathematica, risolvendo direttamente il problema di Cauchy

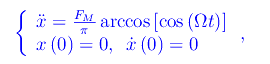
ottenendo una soluzione molto complicata (almeno formalmente) che non riportiamo. Tracciamo poi il grafico in fig. fig:xnoperiodico.

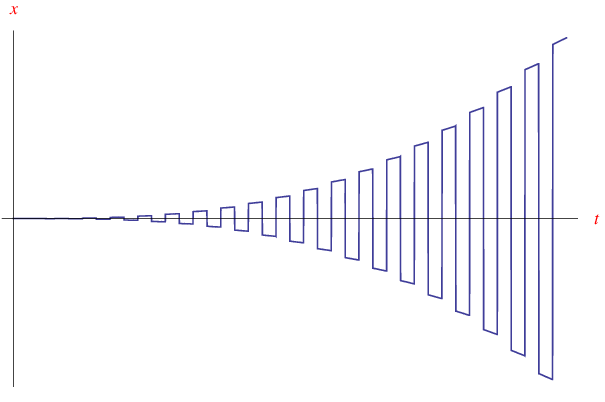
Tags: forza periodica, funzioni circolari inverse, Funzioni periodiche, punto materiale

Articoli correlati