» Esercizi svolti di Matematica e Fisica

[¯|¯] Infinitesimi ed infiniti (Lezione 1)

Febbraio 21st, 2017 | by Marcello Colozzo |

---

Sia f una funzione reale di una variabile reale definita in un sottoinsieme X di R:

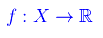
Se x₀ è un punto di accumulazione per X, sussistono le seguenti definizioni:
Definizione 1
f è un infinitesimo in x₀ (o per x->x₀) se

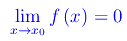
Definizione 2
f è un infinito in x₀ (o per x->x₀) se

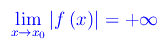
Alcuni esempi di infinitesimi:
Esempio 1
La funzione f(x)=sinx è un infinitesimo negli infiniti punti

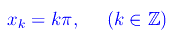
Esempio 2
La funzione f(x)=x*sin(1/x) non è definita in x=0, tuttavia:

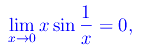
per cui x*sin(1/x) è un infinitesimo nel predetto punto.

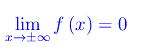
Esempio 3
La funzione f(x)=1/x è un infinitesimo per x->+oo e per x.>-oo, giacché:

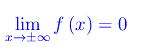
Alcuni esempi di infiniti:

Esempio 4
La funzione f(x)=csc x è un infinito negli infiniti punti

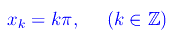
Esempio 5
La funzione f(x)=1/x è un infinito in x=0.

Infinitesimi confrontabili. Il concetto di ordine

Se x₀ è un qualunque punto di accumulazione per X, resta definito l'insieme

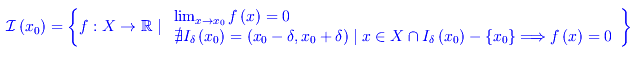
che si identifica con la classe degli infinitesimi in x₀ non definitivamente nulli intorno a tale punto.

Ciò premesso, comunque prendiamo due infinitesimi della predetta classe il confronto tra f e g si realizza calcolando il limite del rapporto f/g:

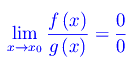
Si presentano i seguenti casi:

1. Il rapporto è un infinitesimo:
   
   Significa che f(x) tende a zero più rapidamente di g(x). Diremo allora che f(x) è un infinitesimo di ordine superiore a g(x).
2. Il rapporto è un infinito:
   
   Significa che g(x) tende a zero più rapidamente di f(x). Diremo allora che f(x) è un infinitesimo di ordine inferiore a g(x).
3. Il rapporto converge a un limite non nullo:
   
   Significa che f(x) e g(x) tendono a zero con la medesima rapidità. Diremo allora che f(x) e g(x) sono infinitesimi dello stesso ordine.
4. Il rapporto è non regolare
   
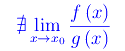
   Esempio 6
   Siano
   
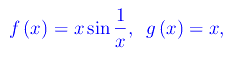
   infinitesimi della classe I(0). Abbiamo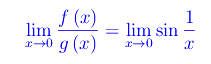
   
   e tale limite non esiste.
   
   
   
   
   
   
   
   
   In casi come questi spostiamo la nostra attenzione sul rapporto |f(x)|/|g(x)|, calcolando:
   
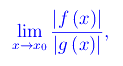
   per cui si presenta uno dei seguenti sottocasi:
   • 
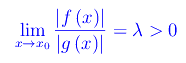
     Qui f(x) e g(x) sono infinitesimi dello stesso ordine.
   • 
     e diremo che f(x) è un infinitesimo di ordine inferiore a g(x).
   • Il rapporto|f(x)|/|g(x)| è non regolare
     
     ma è definitivamente limitato (intorno a x₀) tra due numeri positivi:
     
     In tale circostanza diremo che f(x) e g(x) sono infinitesimi dello stesso ordine.

In tutti i casi esaminati gli infinitesimi assegnati si dicono confrontabili. Viceversa, si dicono non confrontabili se si verifica la negazione della condizione precedente i.e. il rapporto |f(x)|/|g(x)| non è definitivamente limitato intorno a x0:

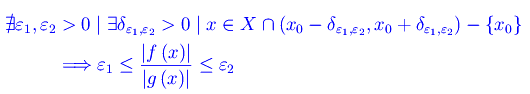
Fa eccezione il seguente caso:

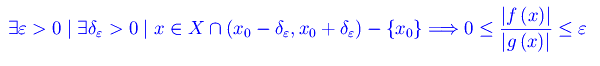
Cioè se il rapporto |f(x)|/|g(x)| ha, intorno a x0, per estremo inferiore lo zero ed è limitato superiormente. In tale circostanza si dice che f(x) è un infinitesimo di ordine non inferiore a g(x). In maniera simile:

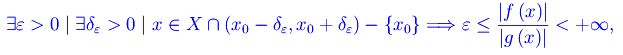
ovvero il rapporto |f(x)|/|g(x)| è definitivamente limitato inferiormente ma non superiormente. Ne consegue che f(x) è un infinitesimo di ordine non superiore a g(x).

---

Tags: infinitesimi, infinitesimi confrontabili, infinitesimi non confrontabili, infiniti, ordine

Articoli correlati