[¯|¯] Corrispondenze tra insiemi
Ottobre 15th, 2014 | by extrabyte |Definizione
Assegnati gli insiemi A e B, dicesi corrispondenza da A verso B, l'applicazione:
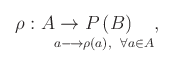
dove P(B) è l'insieme delle parti di B.
In altri termini, una corrispondenza da A verso B è una legge che associa univocamente un elemento di A a un sottoinsieme di B. Si tratta, dunque, di una generalizzazione della nozione di applicazione che, come noto, associa univocamente un elemento di A a un elemento di B. Risulta:

Chiamiamo  immagine di a mediante rho.
immagine di a mediante rho.
Definizione
Per un assegnato a, poniamo per definizione  . Ogni elemento
. Ogni elemento  si chiama corrispondente di a mediante
si chiama corrispondente di a mediante  .
.
Definizione
Siano
 e
e  due corrispondenze da A verso B. Diremo che
due corrispondenze da A verso B. Diremo che  e
e  coincidono se e solo se:
coincidono se e solo se:
Esempio
Se A è l'insieme delle rette dello spazio ordinario, la legge che associa a una retta r l'insieme delle rette parallele ad r è una
corrispondenza:

Per  è
è  , cioè l'insieme delle rette parallelle ad r.
, cioè l'insieme delle rette parallelle ad r.
Definizione
Una corrispondenza è univoca se per ogni  contiene un
contiene un
solo elemento. Cioè  .
.
Una corrispondenza univoca determina in modo naturale un'applicazione:

tale che f(a)=a' essendo a' l'unico elemento di rho(a').
Definizione
Assegnata la corrispondenza
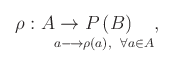
si dice immagine inversa di a' il sottoinsieme di A:

Ciò determina una corrispondenza da B verso A:


La corrispondenza definita sopra si chiama corrispondenza inversa di ρ e si indica con 

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: applicazione, corrispondenza, funzione, immagine, immagine inversa
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











